9. Propiedades del triángulo.

      De todas las propiedades que tienen los triángulos --que son muchas-- hay cinco que pueden considerarse como fundamentales, por que ellas caracterizan distintivamente a tales figuras.

     Teorema (1). En todo trángulo la suma de los ángulos interiores es igual a 2 rectos (=180°).

     En la figura 20 vemos un triángulo arbitrario ABC; las letras que designan los vértices, designan también los ángulos interiores del triángulo. 

     Por el vértice C trazar la recta auxiliar XY, paralela al lado AB del triángulo dado. Es claro que se cumple:

     α + C + β = 180° ...(1)

     Pero A = α por ser alternos internos.

            B = β  por ser alternos internos.

     Las secantes (transversales) son AC y BC, respectivamente.

     Substituir en (1) las igualdades A = α, B = β, para obtener: A + C + B = 180° (= 2 rectos).

     Teorema (2). En todo triángulo un ángulo extremo es igual a la suma de los dos interiores que no le son adyacentes.

     Corolario del anterior. Por que:

     A + B + C = 180°

           γ +  C = 180°              Conclusión: γ = A + B.

     Corolario: Los tres ángulos externos de un triángulo suman 4 rectos = 360°.

     En la figura 21 se tiene: α = B + C

                                            β = C + A

                                            γ = A + B

                   Suman: α + β + γ = 2(A + B + C) = 360°.

     Se llama triángulo isósceles el que tiene dos lados iguales, por lo menos. En particular, son isósceles los triángulos equiláteros, que tienen iguales sus tres lados.

     Teorema (3). En todo triángulo isósceles son iguales los ángulos opuestos a los lados iguales. Recíprocamente todo triángulo con dos ángulos iguales es isósceles.

     Hipótesis: en la figura 22 tenemos que  AC = BC. 

     Trazar la recta auxiliar CX que biseca el ángulo C: lo descompone en dos ángulos iguales ω = φ. Si doblamos el plano a lo largo del eje CX, como ω = φ, el lado CB viene a caer sobre el lado CA y como CA=CB, el punto B viene a coincidir con A. Análogamente, el segmento MB cae sobre MA. Lo que significa que CX es un eje de simétria del triángulo ABC. Vemos así, al doblar la figura, que el ángulo B viene a coincidir con A, lo que prueba que A = B.

     El mismo razonamiento prueba que α = 90°= β y que MB = MA. Lo que significa que el eje CX es perpendicular al lado AB y lo divide en dos partes iguales. Es la mediatriz del lado AB. 

     Se cumple la reciproca: Si A = B entonces AC = BC.

     Porque, si trazamos la perpendicular MX al lado AB, como B = A, al doblar el plano según MX, BC se sobrepone a AC. Lo que significa que el vértice C queda sobre MX y BC = AC.

     Teorema (4). En todo triángulo, a mayor lado se opone mayor ángulo y recíprocamente.

     Del teorema anterior se desprende como corolario que: si un triángulo tiene dos lados desiguales entonces tiene desiguales los ángulos opuestos y viceversa.

     Hipótesis: AC> AB (figura 23).

     Construir AB' = AB y trazar B'B para formar el triángulo auxiliar isósceles ABB', con los ángulos iguales ω = φ. En el triángulo B'BC, el ángulo ω es externo,  y por el teorema (2) se tiene: ω = C + δ. Además: B = φ + δ = ω + δ.

     Por lo tanto: B = C + 2δ por lo tanto B>C.

     Ahora es obvia la recíproca; Si B>C no puede ser AC menor o igual que AB porque sería B menor o igual que C, lo que contradice nuestra hipótesis. Es decir: Si B>C entonces AC>AB.

     Teorema (5). En todo triángulo, un lado cualquiera es menor que la suma de los otros dos lados y mayor que su diferencia.

     Basta demostrar que el mayor lado AC (figura 24) es menor que la suma de los otros dos. Como antes, construir AB' = AB. En el triángulo B'BC, el ángulo α es obtuso y por eso α > δ. Por el teorema anterior, B'C < BC. Se concluye que:

     AC (= AB' + B'C) < AB + BC.

     Falta probar ahora que el lado mediano AB (figura 24) es mayor que la diferencia de los otros dos. Pero esto es obvio, pues la desigualdad obtenida se escribe también así: AB > AC - BC.

     De los cinco teoremas demostrados se desprenden algunas consecuencias, que es importante señalar:

     Ninguna verdad empírica enuncia el teorema (1); simplemente, es consecuencia de las definiciones previas de los axiomas, particularmente del axioma 5 de euclides. El teorema (2) es corolario de (1); también la proposición que dice que la suma de los ángulos externos de un triángulo vale 360°.

     De (1) se infiere que nungún triángulo puede tener dos ángulos rectos, ni obtusos, ni uno recto y otro obtuso; porque la suma de sus ángulos interiores sería entonces mayor que 2 rectos; lo que significa que todo triángulo debe tener por lo menos, dos ángulos agudos. También se infiere de (1) que el menor ángulo de un triángulo no puede ser mayor de 60°; ni el mayor ángulo puede ser menor de 60°; por que la suma de los tres ángulos interiores resultaría ser mayor ó menor que 2 rectos.

     El teorema (4) se deduce de (3); pero a su vez (3) es corolario de (4); lo que significa que ambos teoremas son equivalentes. De ellos se infiere que todo triángulo equilátero tiene sus tres ángulos iguales; además, por (1), cada uno de esos ángulos mide 60°. Recíprocamente; si los tres ángulos de un triángulo son iguales, ese triángulo es equilátero.

     Todo triángulo rectángulo tiene un ángulo recto; los otros dos son agudos y suman un recto. Los lados que forman el ángulo recto son los catetos del triángulo considerado. El lado opuesto al ángulo recto, llamdao hipotenusa, es el mayor lado, por (4). Y por (5), la hipotenusa es menor que la suma de los catetos; pero el teorema de Pitágoras nos dice que; el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Lo demostraremos después en el árticulo 12.

 

  

8. Simetría Axial.

      La mediatriz de un segmento de recta, es perpendicular a dicho segmento y lo divide en dos partes iguales. En la figura 14 la recta RS es la mediatriz del segmento AB; por lo tanto es perpendicular al segmento; el punto M (donde la mediatriz corta al segmento) es el punto medio del segmento AB.

     Se dice también que los puntos A y B son simétricos respecto a la recta RS, que viene a ser el eje de simetría del segmento AB. En otras palabras: dos puntos son simétricos respecto a una recta, si dicha recta es la mediatriz del segmento que definen esos dos puntos.

     Obviamente, si B es el simétrico de A, entonces A es el simétrico de B.

     Todo punto del eje de simetría es simétrico de sí mismo. Por ejemplo: el punto M de la figura 14. 

     Si A no está sobre el eje de simetría, su simétrico B tampoco lo está; pero si A está sobre el eje de simetría, su simétrico es A mismo.

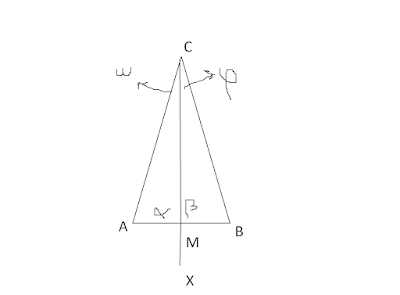
      Si doblamos el papel a lo largo de la recta RS y juntamos las dos caras del papel así doblado, los puntos A y B se confunden en uno solo. Aprovechando este hecho, cualquier punto P sobre la recta RS, donde se dobló el papel, si lo unimos con los puntos A y B, los segmentos que resultan son iguales: PA = PB. Es más, se ha demostrado que los ángulos α y β son iguales, lo cual se expresa diciendo que el eje de simetría es bisectriz del ángulo APB.

     Se dice que una figura tiene un eje de simetría, cuando cada punto de la figura es el simétrico (respecto del eje considerado) de otro punto de la figura. Por ejemplo, la bisectriz de un ángulo es un eje de simétria de ese ángulo. 

     Dos figuras (F) y (F'), son simétricas respecto del eje XY, si cada punto de la primera tiene por simétrico un punto de la segunda, y viceversa. Por ejemplo, los dos triángulos que vemos en la figura 15.

     Dos figuras simétricas son iguales: basta doblar el papel a lo largo del eje de simetría para hacer que las dos figuras coincidan.

 EJERCICIOS.

     1. Si una recta corta a una de dos paralelas, también corta a la otra. Por que, si nola cortara, tendríamos dos paralelas a una misma recta, pasando por un mismo punto, lo que contradice el axioma de Euclides.-Haga el lector la figura y trate los detalles.

     2. Demostrar el teorema que dice: Dos rectas paralelas a una tercera son paralelas entre sí. Explicar todos los detalles hasta comprenderlos.

     3. Si el suplemento del ángulo A es 5A, decir ¿cuánto mide A? Respuesta: A=  . Si el complemento del ángulo X es 4X, decir cuánto mide X? Respuesta: X=  .

     4. Construir dos ángulos opuestos por el vértice. Si uno de ellos gira media vuelta en torno del vértice, debe ir a coincidir con el otro; lo que prueba que son iguales.

     5. En la figura 16 (figura pendiente) vemos tres rectas concurrentes. Contestar: ¿Cuánto suman los tres ángulos no-consecutivos: x, y, z? Respuesta: x+y+z=180°. ¿Por qué?

     6. En la figura 17 (figura pendiente) vemos dos ángulos adyacentes cuyo vértice es Q: los ángulos α y ω suman un llano: α + ω= 180°. Trazar las bisectrices QR y QS: demostrar que ellas forman un ángulo recto: son perpendiculares.

     7. Definir la simetría central en un plano: ¿cuándo decimos que dos puntoss, A y B, son simétricos respecto de un punto Q? ¿Cuál es el centro de simetría de esos dos puntos? ¿Cuándo decimos que una figura plana admite un centro de simetría? ¿Qué pasa si dicha figura gira 1/2 vuelta en torno de su centro de simetría? ¿Por qué decimos que el punto medio de un segmento de recta, es el centro de simetría de todo el segmento?

     8. Contestar: ¿Cuándo decimos que dos figuras,  (F) y (F'), son simétricas respecto de un centro, Q? Igualdad por razón de simetría: ¿Por qué decimos que dos figuras simétricas son iguales o congruentes? Poner ejemplos.

     9. Estudiar el teorema fundamental del paralelismo. Analizar la demostración hasta comprenderla claramente.

     10. En la figura 18 (figura pendiente) las rectas AB y CD son paralelas. Contestar: ¿Qué relación existe entre los ángulos v, x? ¿Cómo son entre sí los ángulos x, z? ¿Cuánto suman los ángulos u, v? Respuesta: (a) Los ángulos v, x son__________________________________________________.

                   (b) Se cumple x=z por ser________________________________________________.

                   (c) u + v = 180° porque__________________________________________________.

     11. Ángulos con lados paralelos, respectivamente. Demostrar que tales ángulos son iguales o suplementarios. ¿Cuándo son iguales o cuándo son suplementarios?

     12. Dibujar dos rectas perpendiculares a una tercera, y demostrar que esas dos rectas son paralelas entre sí. Explicarlo con toda claridad.

     13. Ángulos con lados perpendiculares. En la figura 19 (figura pendiente) vemos dos ángulos agudos α y β, con sus lados perpendiculares respectivamente. Demostrar que α = β.

     14. Extender el teorema anterior (y su demostración) al caso en que ambos ángulos son obtusos, siendo los lados del primero perpendiculares al segundo. ¿Qué pasa si uno de los ángulos es agudo y el otro obtuso?

     15. Definir la simetría axial en un plano y estudiar sus propiedades: puntos que son simétricos de sí mismos, igualdad por razón de simetría,... Poner ejemplos.

     16. Decir: ¿Cuántos ejes de simetría tiene dos rectas que se cortan? Dibujar esos ejes y contestar: ¿qué ángulos forman entre sí? Comparar con el ejercicio número 6.

7. Ángulos con lados perpendiculares.

      Un corolario importante del primer teorema del paralelismo dice: dos rectas perpendiculares a una tercera, son paralelas entre sí. Porque, si AB y CD son perpendiculares a la recta RS, los ángulos alternos internos, marcados en la figura 10

     son rectos y por eso son iguales. Conclusión AB y CD son paralelas. (En la figura 10 RS es secante a las rectas AB y CD).

     Se sigue el teorema que dice: Si los lados de un ángulo son perpendiculares a los de otro, ambos ángulos son iguales o suplemnetarios: son iguales si ambos son agudos u obtusos; son suplementarios si uno es agudo y el otro obtuso. 

     En la figura 11 los ángulos agudos α y β tienen sus lados respectivamente perpendiculares: los lados del ángulo α son perpendiculares a los del ángulo β. Trazar las rectas BP' y BQ', perpendicularres a BR y BS, respectivamente.

     Por el corolario anterior, BP' y AP son paralelas, también lo son BQ' y AQ. Los ángulos α1 y α son iguales por tener sus lados directamente paralelos: α1 = α.

     Vemos en la figura (verde) anterior que se cumple:

     α1 + ω = 90° (ángulo recto).

     ω + β = 90° (ángulo recto).

     α1 + ω = ω + β, por lo tanto α1 = β.

     Las igualdades α1 = α y α1 = β nos dan α = β, lo que se quería demostrar.

     Consideremos ahora la figura 12 donde el ángulo α (obtuso) tiene sus lados perpendiculares a los de β (agudo). Vamos a demostrar que α y β son suplementarios. 

     Prolongando hacia atrás el lado AP, formamos el ángulo α1 = β (demostrado antes). Como α1 y α son suplementarios, deben serlo también α y β; es decir: α + β = 180°.

     Finalmente, en la figura 13 los ángulos α y β son obtusos y tienen sus lados perpendiculares, mutuamente. Si prolongamos hacia atrás el lado AP, se forma el ángulo α1 cuyo suplemento es β (demostrado antes). Se sigue fácilmente que α = β.

6. Ángulos con lados paralelos.

      Dos rectas paralelas y orientadas en el mismo sentido, son directamente paralelas; pero si están orientadas en sentidos opuestos, son inversamente paralelas.

     Sean dos ángulos α y β con lados directamente paralelos, fig. 7. Los lados de α son paralelos directamente a los lados de β. Prolongar atrás de sus vértices los lados de ambos ángulos, para formar el nuevo ángulo φ de la figura.

     α = φ por ser correpondientes entre AY y BV.

     β = φ por ser correspondientes entre AX y BU.

     Conclusión: α = β. Son iguales dos ángulos cuyos lados son directamente paralelos.

En la figura 8 vemos doe ángulos cuyos lados son inversamente paralelos. Los lados de α son inversamente paralelos a los de β. Considerar el ángulo auxiliar φ.

     

     α = φ por ser correpondientes entre las paralelas AX y BU.

     β = φ por ser alternos internos entre las paralelas AY y BV. Conclusión: α = β. Son iguales dos ángulos cuyos lados son inversamente paralelos.

     En la fig. 9 vemos dos ángulos cuyos lados guardan paralelismo mixto. 

     Un lado α es directamente paralelo a un lado de β; pero del otro laso de α es inversamente paralelo al otro lado de β. 

     Se considera el ángulo auxiliar φ.

     α = φ por tener sus lados directamente paralelos

     β + φ = 180° por construcción de φ. 

     Conclusión: β + α = 180°. Los ángulos son suplementarios. 

 

      

5. Teorema fundamental del paralelismo.

     Cuando dos rectas AB y CD son cortadas por una secante RS, como en la figura de abajo, se forman ocho ángulos que se clasifican por parejas, como sigue:

     2 y 6, 4 y 8, 1 y 5, 3 y 7 son pares de ángulos correspondientes. 3 y 6, 4 y 5 son pares de ángulos alternos internos. 1 y 8, 2 y 7 son pares de ángulos alternos externos.

     Hemos señalado ocho pares de ángulos. Fácil es convencernos de que, si los ángulos de un par son iguales entre sí, también son iguales los ángulos de los pares restantes. Por ejemplo, la igualdad de un par de ángulos alternos internos implica la igualdad del otro par; también implica la igualda de los cuatro pares de ángulos correspondientes y la de los dos pares de alternos externos. (Tarea moral: demuéstrelo el lector).

     En la figura rosa (anterior) las rectas AB y CD pueden ser paralelas o no serlo. Pero, si las rectas son paralelas, entonces son iguales todos los pares de ángulos alternos internos y alternos externos y correspondientes. Recíprocamente: si los ángulos de un par son iguales (caso en que son iguales los de cada par) entonces las rectas son paralelas. 

     Teorema(1). Si los ángulos alternos internos son iguales, entonces las rectas son paralelas.

     Hipótesis: 3 = 6 (el ángulo en 3 es igual al ángulo en 6), por lo tanto 4 = 5 (el ángulo en 4 es igual al ángulo en 5).

     Los ángulos alternos internos son iguales.

     Sea O el punto medio del segmento PQ de la secante, comprendido entre las rectas AB y CD. Si hacemos que toda la figura gire media vuelta en su plano, en torno del punto O, por la igualdad de los ángulos alternos internos, la recta AB viene a ocupar el lugar de la recta CD y viceversa. Y la secante viene a caer invertida sobre sí misma. Lo que significa que O es un centro de simetría de la figura. Por lo tanto, si las rectas AB y CD tuvieran un punto común H a la derecha --digamos-- de la secante RS, por simetría tendrían otro punto común G --el simétrico de H-- a la izquiersa de la secante RS. Por el axioma 1, las dos rectas AB y CD serían una sola recta. Es decir: si AB y CD tienen un punto común entonces coinciden. 

     Conclusión: las rectas AB y CD son paralelas.

     Teorema (2). Si las rectas son paralelas entonces son iguales los ángulos alternos internos.

     Hipótesis: AB es paralela a CD, (figura anterior).

     Si α ≠ ω, construir α' = ω, trazando por P la recta A'B'. Como α' = ω, por el teorema anterior, A'B' es paralela a CD. Tendríamos así por el punto P dos paralelas a una misma recta CD; lo que contradice el axioma 5. Esto significa que no puede ser α ≠ ω. 

     Conclusión: α = ω: igualdad de los ángulos alternos internos.

4. Simetría central.

     Dados los puntos A y B, trazar el segmento AB cuyos extremos son esos dos puntos: el punto medio Q del segmento AB se llama centro de simetría de los puntos A y B. Estos dos puntos son simétricos, el uno del otro, respecto del punto Q.

 

     En la figura anaranjada los puntos A y B son simétricos repecto del punto Q, que es el punto medio del segmento AB. Es suficiente un giro o ratación de media vuelta en torno del centro de simetría, Q, para que el punto A pase a ocupar la posición de B, o viceversa: para que B pase a ocupar la posición de A.

     Decimos que una figura (F) admite un centro de simetría, Q, cuando cada punto de (F) tiene por simétrico otro punto de (F) respecto del centro Q. Por ejemplo: el punto medio o centro de un segmento de recta, AB, es su centro de simetría, porque todo punto del segmento tiene por simétrico otro punto del propio segmento, respecto del centro Q. Toda figura que admite un centro de simetría, se sobrepone a ella misma mediante un giro o rotación de media vuelta en torno del centro de simetría.

     Se dice que dos figuras son simétricas respecto de un centro de simetría, Q, cuando cada punto de la primera tiene por simétrico un punto de la segunda, respecto de Q. Y viceversa: cada punto de la segunda tiene por simétrico un punto de la primera, respecto de Q.

     En la figura amarilla el triángulo ABC tiene por simétrico al triángulo A'B'C'; el centro de simetría es O. Cada punto del triángulo ABC tiene por simétrico un punto del triángulo A'B'C' y viceversa. Es sificiente un giro o rotación de media vuelta en trono del centro de simetría, para que cada uno de estos triángulos vaya a sobreponerse el otro, punto por punto. Lo  que prueba que esos dos triángulos son iguales o congruentes.

     (Dos figuras se llaman iguales o congruentes cuando es posible sobreponerlas--sin deformarlas-- de modo que vengan a coicidir en todos sus puntos.)

     Dos figuras simétricas son iguales o congruentes.

     Todo punto de una recta es centro de simétria de toda la recta. Los ángulos opuestos por el vértice son simétricos respecto del vértice común, lo que prueba que dichos ángulos son iguales.

     

3. Perpendiculares y oblicuas.

     Dos rectas que se cortan forman cuatro ángulos. En la figura los ángulos A y B son adyacentes: mientras que A y C son opuesto por el vértice.

     Los ángulos opuestos por el vértice son iguales. Los ángulos adyacentes son suplementarios: suman 2 rectos o sea 180°. Si los 4 ángulos son todos iguales cada uno es recto (=90°), como sucede en la siguiente figura.

     Entonces la rectas son perpendiculares. Dos rectas perpendiculares se cortan formando cuatro ángulos rectos. Pero si las rectas son oblicuas forman dos pares de ángulos iguales, opuestos por el vértice; agudos los de un par y obtusos los del otro par, como se ve en la figura, amarilla, anterior. Para demostrar que los ángulos opuesto por el vértice son iguales, observamos de la figura amarilla que si ponemos:

• A + B = 180° (ángulo llano)
• B + C = 180° (ángulo llano)
• Entonces A + B = B + C, por lo tanto A = C.

 

2. Clasificación de ángulos.

       Una semi-recta que gira en torno de un punto de origen describe un ángulo. Puede suponerse también que el ángulo es la zona del plano comprendida entre dos semi-rectas que tienen un origen común. 

     Para medir ángulos, la unidad natural es el ángulo de una vuelta (=360°). El ángulo de una vuelta se divide en 360 partes iguales, cada una de las cuales viene a ser el ángulo de 1° (un grado). Queda así definido el ángulo de 1° como la 360-ava parte de una vuelta.

 

     

     El ángulo de una vuelta (o 360°). La mitad del ángulo de una vuelta es el ángulo llano (de 180°).

     La mitad del ángulo llano es el ángulo recto (de 90°).

     Un ángulo mayor que uno recto es un ángulo obtuso.

     Un ángulo menor que uno recto es águdo.

     1 vuelta = 2 llanos = 4 rectos. En el estudio de los polígonos, que veremos después, sólo se consideran ángulos menores que el de una vuelta. Estos ángulos se clasifican en comparación con el ángulo llano, como sigue:

• (a) ángulo cóncavo: mayor que un llano.
• (b) ángulo convexo: menor que un llano.

     Los ángulos convexos (menores que el ángulo llano) se clasifican en comparación con el ángulo recto, como sigue:

• (c) ángulo obtuso: mayor que un recto.
• (d) ángulo agudo: menor que un recto.                      

     En las figuras anteriores se ilustra lo dicho.

Ejercicios (tarea, moral).

     1. Contestar: ¿qué es un ángulo llano? ¿Qué es un ángulo concavo? ¿Qué es un ángulo convexo? ¿Qué es un ángulo recto? ¿Qué es un ángulo obtuso? ¿Qué ángulos miden menos que 1 recto?

     2. Contestar: ¿cuántos ángulos llanos mide el ángulo de 1 vuelta? ¿Cuántos rectos mide un llano? ¿Cuántos ángulos rectos hay en 1 vuelta?

     3. Contestar: ¿cuántos ángulos de 15° hay en un llano? ¿Cuántos ángulos de 5° contiene 1 recto? ¿Cuántos ángulos de 3° hay en 1/2 ángulo recto? ¿Cuántos ángulos de 12° hay en una vuelta?

1. Axiomas de la geometría.

 Geometría del plano

     

      Imaginamos una línea recta como teniendo extención infinita en dos sentidos opuestos. Si solamente se extiende en un sentido, tendremos una semi-recta (un rayo). 

     Un segmento de recta es la porción de recta comprendida entre dos de sus puntos, que son los extremos del segmento.

     No se definen los conceptos de punto, recta y plano (aunque si se pueden definir), pero se usan conforme a los axiomas o postulados siguientes:

• Dos puntos definen una recta: la que contiene esos dos puntos. Quiere decir que por dos puntos daos se puede siempre trazar una recta y sólo una.
• Una recta que pasa por dos puntos de un plano está totalmente contenida en ese plano.
• Toda recta contenida en un plano lo divide en dos regiones distintas, que se extienden a uno y otro lados de la recta considerada, y se caracterizan como sigue:

(a) dos puntos situados en una cualquiera de esas regiones definen un segmento totalmente contenido en dicha región:

(b) dos puntos situados en regiones opuestas definen un segmento que corta a la recta dada. 

•  Tres puntos que no están en una misma recta definen un plano: el que  contiene esos tres puntos.

•  Axioma de Euclides: Por un punto exterior a una recta se puede trazar una paralela y sólo una a dicha recta.

(Un buen ejeercicio es ilustrar con figuras los axiomas anteriores).

     Los axiomas se admiten sin demostración. De los axiomas que hemos puesto se desprenden algunas consecuencias inmediatas. Por ejemplo, del axioma del primer punto se infiere que dos rectas distintas no pueden tener sino un solo punto común o ninguno.- Dos rectas sin punto común y en un mismo plano, son paralelas.- Del axioma del segundo punto se desprende que, si una recta no está contenida en un plano, ella sólo puede encontrar al plano en un punto o en ninguno. En el segundo caso se dice que la recta es paralela al plano.

     El axioma del cuarto punto se enuncia también diciendo: Dos rectas que se cortan definen un plano, que las contiene o también así:

     Una recta y un punto ajeno a dicha recta, definen un plano que contiene a ambos. (Ejecicio: explicar ¿por qué?).

     La geometría que vamos a estudiar aquí es la Geometría Plana, es decir: geometría de las figuras que podemos trazar en un plano (también geometría Euclidiana).

     Se dice que  dos rectas del plano son paralelas cuando, por más que se prolonguen, no llegan a encontrarse. En otras palabras: son paralelas dos rectas del plano que no tienen ningún punto común.

     Esta definición presenta el inconveniente de impedir que una recta pueda ser considerada como paralela a sí misma. Por eso definimos, mejor el paralelismo, diciendo:

     "Si dos rectas tienen un punto común entonces coinciden en todos sus puntos"

     En vista de esta definición, dos rectas son paralelas en los dos casos siguientes:

(a) cuando no tienen punto común.

(b) cuando ambas se reducen a una sola.

     Se desprenden estas dos consecuencias:

(c) toda recta es paralela a sí misma.

(d) dos rectas paralelas a una tercera son paralelas entre sí.

     Esta última propiedad resulta de la definición de paralelismo y del axioma de Euclides. Porque, si dos rectas (r) y (a) son paralelas a una recta (t) y tuvieran un punto común, entonces por el axioma de Euclides, ellas serían una sola recta. Lo que significa, por la definición de paralelismo, que (r) y (s) son paralelas entre ellas.