9. Propiedades del triángulo.

      De todas las propiedades que tienen los triángulos --que son muchas-- hay cinco que pueden considerarse como fundamentales, por que ellas caracterizan distintivamente a tales figuras.

     Teorema (1). En todo trángulo la suma de los ángulos interiores es igual a 2 rectos (=180°).

     En la figura 20 vemos un triángulo arbitrario ABC; las letras que designan los vértices, designan también los ángulos interiores del triángulo. 

     Por el vértice C trazar la recta auxiliar XY, paralela al lado AB del triángulo dado. Es claro que se cumple:

     α + C + β = 180° ...(1)

     Pero A = α por ser alternos internos.

            B = β  por ser alternos internos.

     Las secantes (transversales) son AC y BC, respectivamente.

     Substituir en (1) las igualdades A = α, B = β, para obtener: A + C + B = 180° (= 2 rectos).

     Teorema (2). En todo triángulo un ángulo extremo es igual a la suma de los dos interiores que no le son adyacentes.

     Corolario del anterior. Por que:

     A + B + C = 180°

           γ +  C = 180°              Conclusión: γ = A + B.

     Corolario: Los tres ángulos externos de un triángulo suman 4 rectos = 360°.

     En la figura 21 se tiene: α = B + C

                                            β = C + A

                                            γ = A + B

                   Suman: α + β + γ = 2(A + B + C) = 360°.

     Se llama triángulo isósceles el que tiene dos lados iguales, por lo menos. En particular, son isósceles los triángulos equiláteros, que tienen iguales sus tres lados.

     Teorema (3). En todo triángulo isósceles son iguales los ángulos opuestos a los lados iguales. Recíprocamente todo triángulo con dos ángulos iguales es isósceles.

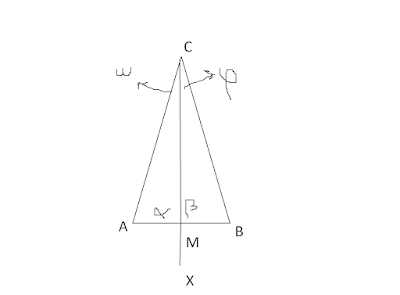
     Hipótesis: en la figura 22 tenemos que  AC = BC. 

     Trazar la recta auxiliar CX que biseca el ángulo C: lo descompone en dos ángulos iguales ω = φ. Si doblamos el plano a lo largo del eje CX, como ω = φ, el lado CB viene a caer sobre el lado CA y como CA=CB, el punto B viene a coincidir con A. Análogamente, el segmento MB cae sobre MA. Lo que significa que CX es un eje de simétria del triángulo ABC. Vemos así, al doblar la figura, que el ángulo B viene a coincidir con A, lo que prueba que A = B.

     El mismo razonamiento prueba que α = 90°= β y que MB = MA. Lo que significa que el eje CX es perpendicular al lado AB y lo divide en dos partes iguales. Es la mediatriz del lado AB. 

     Se cumple la reciproca: Si A = B entonces AC = BC.

     Porque, si trazamos la perpendicular MX al lado AB, como B = A, al doblar el plano según MX, BC se sobrepone a AC. Lo que significa que el vértice C queda sobre MX y BC = AC.

     Teorema (4). En todo triángulo, a mayor lado se opone mayor ángulo y recíprocamente.

     Del teorema anterior se desprende como corolario que: si un triángulo tiene dos lados desiguales entonces tiene desiguales los ángulos opuestos y viceversa.

     Hipótesis: AC> AB (figura 23).

     Construir AB' = AB y trazar B'B para formar el triángulo auxiliar isósceles ABB', con los ángulos iguales ω = φ. En el triángulo B'BC, el ángulo ω es externo,  y por el teorema (2) se tiene: ω = C + δ. Además: B = φ + δ = ω + δ.

     Por lo tanto: B = C + 2δ por lo tanto B>C.

     Ahora es obvia la recíproca; Si B>C no puede ser AC menor o igual que AB porque sería B menor o igual que C, lo que contradice nuestra hipótesis. Es decir: Si B>C entonces AC>AB.

     Teorema (5). En todo triángulo, un lado cualquiera es menor que la suma de los otros dos lados y mayor que su diferencia.

     Basta demostrar que el mayor lado AC (figura 24) es menor que la suma de los otros dos. Como antes, construir AB' = AB. En el triángulo B'BC, el ángulo α es obtuso y por eso α > δ. Por el teorema anterior, B'C < BC. Se concluye que:

     AC (= AB' + B'C) < AB + BC.

     Falta probar ahora que el lado mediano AB (figura 24) es mayor que la diferencia de los otros dos. Pero esto es obvio, pues la desigualdad obtenida se escribe también así: AB > AC - BC.

     De los cinco teoremas demostrados se desprenden algunas consecuencias, que es importante señalar:

     Ninguna verdad empírica enuncia el teorema (1); simplemente, es consecuencia de las definiciones previas de los axiomas, particularmente del axioma 5 de euclides. El teorema (2) es corolario de (1); también la proposición que dice que la suma de los ángulos externos de un triángulo vale 360°.

     De (1) se infiere que nungún triángulo puede tener dos ángulos rectos, ni obtusos, ni uno recto y otro obtuso; porque la suma de sus ángulos interiores sería entonces mayor que 2 rectos; lo que significa que todo triángulo debe tener por lo menos, dos ángulos agudos. También se infiere de (1) que el menor ángulo de un triángulo no puede ser mayor de 60°; ni el mayor ángulo puede ser menor de 60°; por que la suma de los tres ángulos interiores resultaría ser mayor ó menor que 2 rectos.

     El teorema (4) se deduce de (3); pero a su vez (3) es corolario de (4); lo que significa que ambos teoremas son equivalentes. De ellos se infiere que todo triángulo equilátero tiene sus tres ángulos iguales; además, por (1), cada uno de esos ángulos mide 60°. Recíprocamente; si los tres ángulos de un triángulo son iguales, ese triángulo es equilátero.

     Todo triángulo rectángulo tiene un ángulo recto; los otros dos son agudos y suman un recto. Los lados que forman el ángulo recto son los catetos del triángulo considerado. El lado opuesto al ángulo recto, llamdao hipotenusa, es el mayor lado, por (4). Y por (5), la hipotenusa es menor que la suma de los catetos; pero el teorema de Pitágoras nos dice que; el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Lo demostraremos después en el árticulo 12.